Population model codling moth

Please note: the model is currently still in the beta phase. In the next few months the model will be tested and evaluated by us, so that settings can always change.

The model is based on the codling moth model developed in Switzerland by Graf, Höhn, Höpli and Kuske 2018. It is a population model, i.e. all stages beginning with the codling moth pupae in spring are simulated. At the start of the model 100 pupae are assumed.
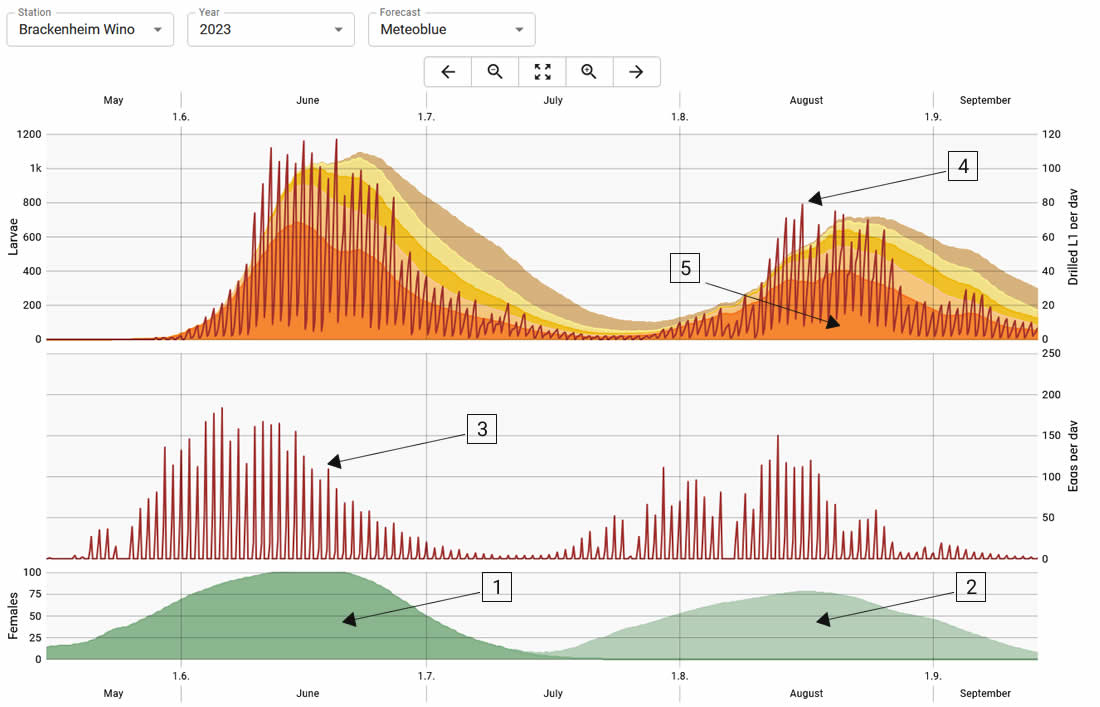
Special attention has been paid to the egg deposition, the L1 larvae and the fresh holes drilled by the L1 larvae. The egg deposition and the incisions are given per day. The occurrence of the moths (females) and the larval stages are shown as a sum and their development over time.

Starting point (Biofix):

If no settings are made in the model, the model starts calculating the temperature sum (T0 > 10°C, mean value 417 DD, SD 63) for the hatching of codling moth slices on 1 January. The codling moth pupae develop at three different speeds. This depends on the exposure of the pupae to the sun. At the moment, the actual solar radiation is not yet used to calculate the developmental speed of the fast and medium codling moth pupae, but flat-rate supplements are calculated. However, this will soon be changed to the method published by Graf et. al. 2003, which includes solar radiation.
First tests have shown that the calculation of the flight start with this method works very well. This is especially true for the region of Southern Germany and the Alte Land. If there should be differences in other regions, it is possible to start the start of the model manually by entering the flight start (pheromone trap). Decisive here are the first captured butterflies in the region. So please ask your advisors for this date.

Female fertility

According to studies by Graf et al. 2018, fertility is highest at the beginning of their oviposition activity (after the pre-oviposition phase) and then decreases significantly over time. Graf et. al. 2018 work with a Weibull distribution. We have approximated this with an Erlang distribution (To > 10°C, mean value 115 DD, SD 66).

Egg deposition

The codling moth females lay their eggs in the evening hours during twilight. The intensity of egg deposition depends on 3 factors

1. Time of day: the eggs are laid before and after sunset. For the intensity of the egg laying activity over time we have used a normal distribution. The highest intensity occurs at the time of sunset (mean value 2 hours, SD 0.5 hours).
2. Weather conditions: the egg laying intensity depends on the temperature. Below 14°C no eggs are laid. The optimum temperature is 23 to 25°C. Above 31°C no eggs are laid. In case of precipitation, egg laying is interrupted.
3. Fertility: see above

Egg and larval development

The following parameters are used for the development of the eggs and the different larval stages

Each stage was subjected to two speeds of development. On the one hand, the temperature sum was calculated on the basis of the measured air temperature, and on the other hand, a supplement was calculated for the part of the population that is exposed to higher solar radiation (analogous to post-diapause development).

Second generation of codling moth

Currently only the first generation of codling moth is simulated. The second generation will follow soon.

Calculation method

The fruitweb codling moth model was developed on the basis of the time varying distributed delay model (Manetsch 1976). This makes it possible to calculate the development of each simulated individual with a time interval of 30 minutes. Therefore, the transitions between the different stages (egg, larva, pupa and adult) are not normally distributed but follow an Erlang distribution.

Literature

T.J. Manetsch (1976). Time-varying distributed delays and their use in aggregative models of large systems. IEEE Transactions on Systems, Man, and Cybernetics 6: 547–553.

B. Graf, H. Höhn, H.U.Höpli und S. Kuske (2018). Predicting the phenology of codling moth, Cydia pomonella, for sustainable pest management in Swiss apple orchards. The Netherlands Entomological Society Entomologia Experimentalis et Applicata 166: 618-627

B. Graf, H.U. Höpli und H. Höhn (2003). Optimizing insect pest management in apple orchards with SOPRA. Bulletin IOBC/SROP, Vol.26 No.11:43-48